#漂亮的几何数学题#正五边形内一点求面积,多个解题思路
2022年数学趣题# 一道来自网友@koko 咨询的趣题:正五边形内一点,连接各顶点,分割面积如下,求未知部分的面积大小。
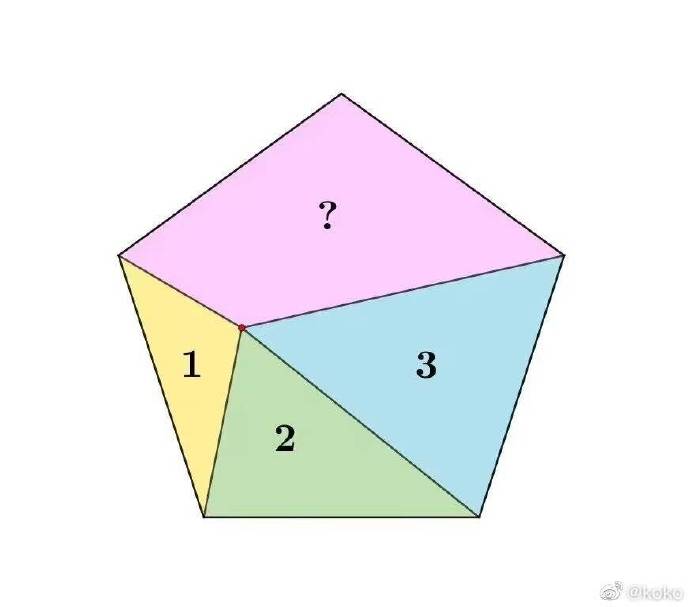
解题方法一:yuange万能通用解法
更一般性的结果。
正n边形内一点,到相邻4顶点(如果是正三边形有2点重合)连线形成的三个相邻三角形,面积分别是a、b、c。
则正n边形面积Sn=1/2n(a+c-2b*cosx)/(1-cosx),x=2PI/n。
S3=a+c+b
S4=2(a+c)
S6=6(a+c-b)
特别地如果a+c=2b,Sn=nb。对此题就是1+3=22,Sn=52=10,S=4。
解:
如图3正n边形内(图是正5边形,正n边形上面加边就是不影响)一点P,S三角形PEA=a,S三角形PAB=b,S三角形PBC=c。求正n边形面积Sn。
对于n大于4,如图3延长EA、CB交于F,正n边形中心O。
角AOB=角FAB=角FBA=x=2PI/n。
S三角形FAB
=S三角形PAF+S三角形PBF-S三角形PAB
=aFA/AB+cFB/AB-b
=(a+c)/(2cosx)-b
=1/2AB(AB*sinx/cosx)
Sn
=n*S三角形OAB
=n1/2AB(ABcos(x/2)/sin(x/2))
=ncos(x/2)/sin(x/2)cosx/sinx*((a+c)/(2cosx)-b)
=n/4*(a+c-2bcosx)/(sin(x/2))^2
=1/2n(a+c-2b*cosx)/(1-cosx)
检验对于正三边形和正四边形都符合此公式。
所以:
Sn=1/2n(a+c-2b*cosx)/(1-cosx),x=2PI/n。
特别的如果a+c=2b,Sn=nb。
评:三角函数是yuange的最爱,图形皆可函数化。
解题思路二:大罕的黄金分割
黄金比,优雅计算
大罕
有跟帖说:此题“由正五边形边长的黄金比,易得所求面积为4”.易得,真的“易得”吗?
把长为1的线段分成两段:x、1-x(x>1-x),满足x∶1=(1-x)∶x,解得x=(√5-1)/2. 我们称这个分割为黄金分割,把Φ=(√5-1)/2称为黄金比.
正五边形与黄金比有着千丝万缕的联系.
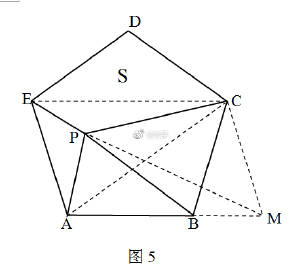
图5为正五边形ABCDE,在△ACE中,由正弦定理,有
EA/EC=sin36°/sin72°=1/(2cos36°)
=(√5-1)/2=Φ.
即正五边形的边与对角线之比是黄金比.
以下作一次有趣的历程:
作平行四边形EAMC,△BMC∽△EAC,
∴BM/AB=BM/BC=EA/EC=Φ. 遇见黄金比.
注意到
S(△PBM)/S(△PAB)=BM/AB=Φ,
⇒ S(△BMP)=3Φ,再见黄金比.
设△DEC面积为S,
S(△CBM)/S(△CAB)=BM/AB=Φ,
⇒ S(△BMC)=SΦ,又见黄金比.
⇒S(△CPM)=S(△CPB)+S(△CBM)-S(△PBM)=3+SΦ-2Φ,
由此,可用两个方式计算平行四边形EAMC的面积之半:
S(△EAP)+S(△CPM)=1+3+SΦ-2Φ, ①
S(△CAB)+S(△CBM)=S+SΦ, ②
由①、②得:4+SΦ-2Φ=S+SΦ,
解得S=4-2Φ,漂亮的结果!
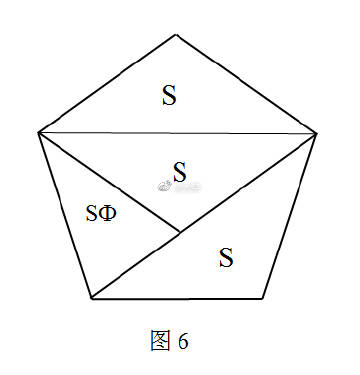
注意到S(正五边形)=3S+SΦ=(3+Φ)S,如图6,
∴S(正五边形)=(3+Φ)(4-2Φ)
=12-2(Φ+Φ^2)=10 (这里用到了Φ+Φ^2=1),
∴S(EPCD)=10-(1+2+3)=4.
优雅计算,斩获成功!
解题思路三:最本质也是最简单的方法 - 大罕
最本质也是最简单的方法,如下文所示。
不禁想起鲁迅(1881-1936)的诗句:“于无声处听惊雷”。此句直接翻译是:从表面沉寂中,听到天上的惊雷(原诗象征着革命春雷的萌动)。
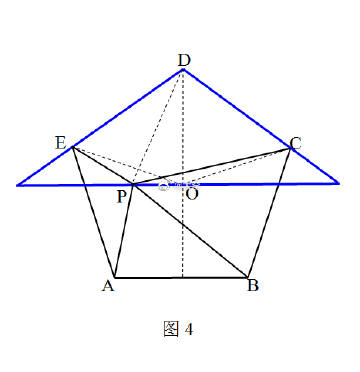
解题灵感的获得,可比喻为:于无声处、百思不解之时,忽然听到“惊雷”。由此大彻大悟。此处的“惊雷”,即等腰三角形一性质:“底边上任一点到两腰距离之和等于一腰上的高。” 解:作直线PO∥AB,交线段AB的中垂线DF于点O,则直线PO、EA、CB围成一个等腰三角形(蓝色),如图3,
作PM⊥EA、PN⊥CB、OG⊥EA,垂足分别为M、N、G,
易知PM+PN=2OG(等腰三角形性质),
⇒S(△APE)+S(△BPC)=2S(△AOE)=1+3=4,
⇒S(△AOE)=2,
∴S(△AOB)=S(△APB)=2,
⇒S(△AOE)= S(△AOB),⇒OG=OF,⇒O是正五边形的中心。
直线PO、DE、EC也围成一个等腰三角形(蓝色),如图4,
同理可知,S(四边形PEDC)=S(△PED)+S(△PDC)=2S(△DOE)=4.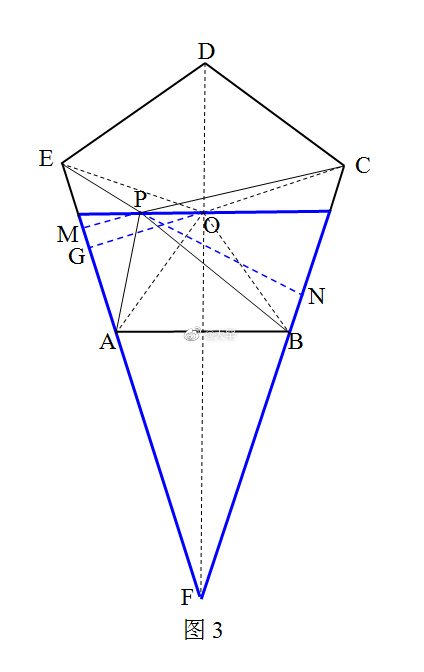
本作品采用 知识共享署名-相同方式共享 4.0 国际许可协议 进行许可。
评论已关闭